M2C2A: Episode 19: Definition of factorial (but about the things most people don't know), an adventure ranging from elementary calculations, to calculus itself.

For this adventure, I will have a friend:
-So now you're involving me?Yes, I am.
Now, to start: "What is a factorial?"
-A factorial? That's easy:
When you say x! (x factorial), you mean the multiplication of all integers bigger than 1 up to itself.
For example, 4! is equal to 2x3x4, or 24,
7! is equal to 2x3x4x5x6x7, or 5040,
and 15!=2x3x4x5x6x7x8x9x10x11x12x13x14x15, or 1,307,674,368,000.
-Whoa, factorials grow fast.
Yes, factorials do grow pretty fast. Here's a list of the factorials of some small integers:

• 0!=1
• 1!=1
• 2!=2
• 3!=6
• 4!=24
• 5!=120
• 6!=720
• 7!=5040
• 8!=40320
• 9!=362880
• 10!=3628800

-But why 0! is equal to 1?
A property about integer factorials is that (x-1)!=x!/x.
So if we make x equal to 1, 0!=1!/1, or simply 1.
-But what about -1!, or -2!, or...
If x=0, we eventually get that -1! is 1/0.
-1/0? That's a problem.
Next, if x=-1, we get that -2!=-1/(1/0), but...
-That is equal to -1/1 * 0/1, or... 0!
That should be right, but calculators will give the answers for all of these values as "INFINITY" or "NEGATED VALUE".
-But we can still try to get our own values, can we?
Actually, that's what M2C2A is all about. And using this formula, -3! should be 1/0, and -4! should be 0... 
-But what about 1.5!, or 7.345!?
Luckily, I don't have to figure that out, because for positive integers, there is a formula for factorials. For positive numbers, it is:
            ∞
(z-1)!= ∫  t^z-1 e^-t dt
           0
-WHAT THE...?!
Don't worry, we'll examine the formula one by one part.
-But wait, why (z-1)! and not z!?
(z-1)! is the same as Γ(z), pronounced as "the gamma function of z".
- Next, what is that thing that looks like a "s"?
It is an integral. It is used mainly in calculus.
-WAIT? ARE WE GOING INTO CALCULUS RIGHT NOW?
Yes. We're going into calculus right now.
-Aww...
Don't worry, it isn't as bad as you think.
-Yeah you say so...
I really don't think it's going to WHOA-RK!
Where are we now?
A world, a very strange world, could be seen. It was a line.
We're in the graph of 2x=y 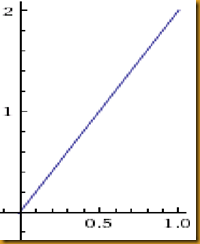. And we're going to get the integral of this.
First, to write "the integral of 2x=y", we're going to use only "2x".
-BUT WHAT THE WHAT, WHERE, OR WHO IS AN INTEGRAL?!
It is only the calculation of the area between the line of a graph and the x-axis.
-Please speak English.
What I said only means this!

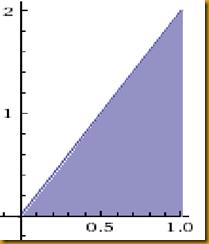
Suddenly, the graph started shaking, and from nothing, something blue appeared, between the bottom line, and the previous line.

The line at the bottom just turned out to be the x-axis. And we need to calculate the area that is below the blue line.
-But what is our range?
Here, x will go from 0 to 1, and we need to get the area of the triangle below 2x=y, or simply, 2x, so we can write this as:
1
∫ 2x dx
0
The 0 and the 1 specify the range, 2x represents the equation for which we will find the area, and dx only specifies the variable (after the d), x.
So, using the formula for the area of a triangle, because the width is 1, and the height is 2, the integral equals...
-1!
Correct, it equals 1. But that would actually be cheating, for how do we get the integral for something more complicated. For example:
1
∫ 4x^3 dx
0
-Hey! It is impossible to define that! The equation isn't a geometrical shape!
That's right...
But incorrect.

A whistle was heard. Suddenly, a seemingly never-ending stampede of something could be heard at a distance.
That something was:

-Paper strips?!

Each paper strip accommodated itself in the graph. They had base 0.25 and height that would accommodate to the graph's height. But many of the graph's space wasn't filled.

-We can't use you to calculate the area, or can we?
We can! Make the base smaller!

Suddenly, the paper strips started to shrink their base to 0.10. But that wasn't enough.

-Shrink even more!
Wait. Couldn't we make the base 0 so everything could fit perfectly?
-No. Or else the area of the strips will disappear!
Exactly! You are beginning to understand infinitesimal calculus!
Let's make the area x:
lim
x->0
-And I thought I had it! What the heck is that?
Don't worry. That only means that x is ALMOST 0, but not exactly.
That is:
THE BASE OF THE STRIPS IS INFINITESIMALLY SMALL.


-But, what is the total area?
The total area is equal to:
1/z
Σ 2kz^2
k=1
-But what is z?
The variable "z" is the base of the strips. 
-And what does the formula mean?!
Σ means that we will be doing a summation, that is, make the variable specified on the lower range, k, be 1, calculate, be 2, calculate, add the previous result... The range of k will be from 1 to 1/z. That is because if the base of the strips is z and we need the value of all the strips bases together to be 1, then the number of strips is 1/z. For example, if our bases measure 0.0625, then the number of strips is 16.
-I get it. But why kz^2?
If the base is z, so the strips adjust to the formula the most possible, their height must be kz, and their area, kz*z=kz^2.
-But what do we do with the values?
First, let z be 0.5 just for this example. Now, the upper range is 2. If you calculate 2kz^2, which is...
-0.5!
...and then let k equal 2, calculate kz^2, and add it to your previous result, you get:-1.5!
Now, if you make z equal 0.25, you will eventually get:...-1.25!Now, let's try for z, 1/50. The answer is:....................-1.02!
And when z=1/9874564?
...................................................................-AGRH!!! THERE MUST BE AN EASIER WAY!
Answer: There is!
Any series that starts in 1 and involves addition (for example, 1+2+3... +99+100) can be expressed as the following formula (x is the last number):
x
Σ k= (x+x^2)/2
k=1
So 1+2+3+4+5=(5+25)/2, or 15, 1+2+3+4+5...+99+100=(100+10000)/2=5050 and 1+2+3+4+5...+9876543209+9876543210=(9876543210+97546105778997104100)/2=48773052894436823655. So...
1/z
Σ 2kz^2
k=1
...is just equal to...-WAIT! THIS ONLY APPLIES WHEN YOU ADD CONSECUTIVE NUMBERS!
Yes, but we can use a property of summations:
  b            b            b
  Σ cd=c  Σ d = d  Σ c
k=a        k=a        k=a
For example,
  3             3
  Σ 3k = 3 Σ k = 3+6+9=3(1+2+3)=3*1+3*2+3*3=3+6+9✓
k=1         k=1
Understood?-Mainly.
Try to see clearly that set of equations and see if you can figure that out.
In the meantime, we can make
1/z
Σ 2kz^2
k=1
Into
       1/z
2z^2 Σ k
       k=1
Into
2z^2(1+2+3...+1/z)
Into
2z^2(1/z+(1/z)^2)/2
Into
z^2(1/z+1/z^2).
Into
z+1!
And that is our general equation!
If we make z=0.5, the equation spits:
-1.5!
If we make z=0.25, the formula says:-1.25!
If z=1/50, then the formula says:
-1+1/50!
And if z is infinitesimally long, then the formula says:
-1!
But why?
Let's recall the length is z.
So the total area is:
z+1
Now, let's say z is so close to 0, we can almost treat it like 0.
So z+1 could be treated as 0+1 or:-1!
That was very interesting, but what do we do with:
          ∞
(z-1)!= ∫  t^z-1 e^-t dt
           0Answer: Use a calculator!
Why?: Because it may be one of the most ridiculous calculations ever!
See you next time!
-The Roaring Thunder

¿Es mi hij@ sobresaliente, superdotado, genio?

Desde que inicié el recorrido en la investigación de este fabuloso mundo de la superdotación, para descubrir cuáles son sus limitaciones y sus ventajas y entender cómo apoyar a mi hijo. He encontrado que las definiciones de niños sobresalientes, son tan diversas y tan diferentes, como los mismos niños, por lo que es difícil entender si estamos todos hablando el mismo idioma y tenemos la misma idea de lo que estamos o queremos apoyar.
Por ejemplo, en México, de acuerdo con la Secretaría de Educación, la definición de niños con Aptitudes Sobresalientes es:

“Los niños con aptitudes sobresalientes son aquellos capaces de destacar significativamente del grupo social y educativo al que pertenecen, en uno o más de los campos del quehacer humano: científico-tecnológico, humanístico-social, artístico y/o de acción motriz, pero al presentar necesidades específicas requieren de un contexto facilitador que les permita desarrollar sus capacidades personales y satisfacer sus necesidades e intereses para su propio beneficio y el de la sociedad.” (Guía para familias. SEP.Programa de Fortalecimiento para la Educación Especial. Pag. 15)

Otra definición sería la de la Asociación Nacional para Niños Superdotados (Estados Unidos), (la cual ha recibido un sin número de quejas…)

“Los individuos superdotados son aquellos que demuestran niveles superiores de aptitud (definida como una habilidad excepcional para razonar y aprender) o competencia (desempeño documentado o logros superiores al 10% o poco fáciles de lograr) en uno o más dominios. Estos dominios incluyen cualquier area estructurada de actividad con sus propios sistemas de símbolos (por ejemplo, matemáticas, música, lenguaje) y/o un conjunto de habilidades sensorimotoras (por ejemplo, pintura, danza, deportes).”

No se ustedes, pero a mí estas definiciones terminan por parecerme ostentosas y la causa de muchas fricciones en la sociedad. Además fragmentan la definición del niño de acuerdo a sus resultados y no a quién en realidad “ES” en todos los aspectos. Porque ¿a poco un niño es sobresaliente sólo si saca una medalla en una competencia? O sólo hasta que va a la escuela y vemos que le va mejor en los exámenes que a otros. El mismo término “gifted” implica que el niño o la niña tiene algo que otros no tienen y que esto lo hace ser “superior” (o sobresaliente) a sus pares.

Empezando por ahí tenemos problemas.

Desde mi experiencia y mi humilde punto de vista ser sobresaliente no tiene que ver con una inteligencia superior (considerando que la Real Academia de la Lengua Española define como inteligencia la “capacidad de comprender y de resolver problemas”). Para mí, esto tiene que ver con el desarrollo neuronal acelerado… Sí ahí está, lo he dicho, todo mundo piensa que el niño sobresaliente es más inteligente, pero yo creo que es más desarrollado ¿ven la diferencia?.
La realidad de estos niños es muy diferente a la de sus compañeros. Es decir, son niños que por azares del destino genético, se desarrollan prematuramente en las áreas cognoscitivas. Algunos autores comparan este desarrollo intelectual a tener un cableado diferente,

“Los niños excepcionalmente superdotados tienen mentes cableadas en formas que los investigadores prácticamente no pueden describir“ (Extracto de Boy Genius set to become younges-ever grad of Independent Study High School Program. Joe Duggan. Hoagies Gifted)

Este cableado diferente los lleva a tener ventaja en el tiempo que tienen practicando o entendiendo conceptos que sus compañeros todavía no han visto. O lo que es lo mismo, su problema o ventaja es que tiene un desarrollo intelectual asincrónico, su edad mental es superior a su edad cronológica.
Por ejemplo, no creo que nadie piense que un niño de segundo de secundaria sea más inteligente que un niño de segundo de primaria, por el simple hecho de que está viendo más información que el pequeño. Simplemente se encuentran en diferentes etapas del desarrollo y es esperable que pueda hacer otras cosas por lo mismo.
Por eso la definición que me parece más acertada en cuanto a mi experiencia es la del Grupo Columbus.

“La superdotación es un desarrollo asincrónico en el cual se combinan habilidades cognoscitivas avanzadas y una intensidad ampliada, para crear experiencias internas y entendimientos que son cualitativamente diferentes de la norma. Esta asincronía se incrementa conforme mayor sea la capacidad intelectual. El que estos niños sean únicos, los hace particularmente vulnerables y los hace requerir modificaciones en la forma en que se crían, se les enseña y se les aconseja, para que puedan desarrollarse óptimamente”( The Columbus Group, 1991, consultado en, Hoagies Gifted)

Usualmente leo cosas como “Todos los niños son superdotados” o una frase que me gusta mucho y que atribuyen a Albert Einstein,

(no encuentro quién es el autor de esta imagen, si alguien sabe quién es, le agradecería me avisara para darle el crédito apropiado).

La realidad es que sí, todos somos genios en un área u otra del desarrollo humano, a esto se le llama DIVERSIDAD, y es lo que ha hecho grande a la humanidad.

Pero es muy importante entender que cuando hablamos de sobresalientes estamos hablando de que existen estos niños “diferentes”, en riesgo, y que requieren de apoyo especial para poder florecer.
Es importantísimo entender que ellos no eligieron ser así, nacieron de esta manera y por lo tanto, no tienen la responsabilidad de venir a salvar al mundo, pero sí merecen tener los derechos básicos que tiene cualquier otro niños, entre ellos, el derecho a la educación.
Es por este motivo que como padres y maestros tenemos la responsabilidad de seguir investigando y entender cuáles son las necesidades que derivan de esta diferencia para poderles ofrecer mejores oportunidades de desarrollo intelectual, social y emocional.
-Eva

Recursos:

Guía para padres. http://www.educacionespecial.sep.gob.mx/pdf/tabinicio/2012/guia_para_familias.pdf
La mejor fuente de información sobre niños sobresalientes o superdotados: http://www.hoagiesgifted.org

M2C2A: Episode 16, Can we give a numerical value to 1/0?

Remember when some episodes ago we used P.I.G. (Patterns In Graphs)? We'll do it again.
What happens when you graph 1/x? You get a graph that looks like 2 rotated "L". You can see the closer x gets to 0, the closer y goes to ∞... but that if you look at the positive region!
For positive values of x, 1/x goes approaching ∞. For example:
1/1=1
1/0.1=10
1/0.01=100
...
But for negative values of x, 1/x goes approaching -∞. For example:
1/-1=-1
1/-0.1=-10
1/-0.01=-100
...
So which is it? ∞, or -∞?
It could be both.
Because 1/10^x=10^-x, then, 1/10^-∞ should be equal to 10^-∞ (And 10^-∞ isn't ∞. That would be like saying 10⁶ (1000000, a million) is equal to 6.), right? There are only 2 problems with that:
1) This could work for all bases, 1/10^x=10^-x is only a form of the more universal equation, 1/n^x=n^-x.
2) x^-∞ can't be 0... Or can it?
x¹=x, x⁰=1, but x^-1=1/x, and x^-2=1/x², so does x^-∞=1/x^∞ (which should definitely be larger than infinity if x>1)? Yes!
But what if you divide 1/<A number definitively bigger than infinity? It should give you a number with ∞ 0's...But is this 0? Think about this in this way, if this number had any digits after the 0's, it would have an end, and it would be infinite... So this is 0 after all! (hope I'm not breaking any kind of calculus law or something) But because x^∞ will only be infinite if x>1, the solution set for 1/0 would be 1/x^∞ only when x>1...
But our rule of 1/n^x=n^-x also applies to when x is positive...
So n^∞=1/n^-∞, But is n^-∞ also 0?
As you graph n^x, when x is negative, the values tend to be 0 as x goes down. So the only thing logical is that:
n^-∞=0!
So the solution set for 1/0 would be 1/x^∞ only when x>1 and x<-1.
-The Roaring Thunder

M2C2A: Episode 15, Thanks for all the π, but without an e there's no pie...

(Mayority of article by Wikipedia)
(Graph from Wolfram|Alpha)
(Series from Wolfram|Alpha)
Many of you might have heard of e, but not very well the definition. Here it is (for starters):

e=(1+1/∞)^∞

No really, there's no typo. Well, in the other hand:
If you have the equation (1+1/n)ⁿ, If n is 1, you have (1+1/1)¹, which is equal to 2. If n is 2, you get 2.25. If n is 4, you get 2.44140625... But as you go towards ∞, you get a number closer and closer to e (2.71828182845904523536028747135266249775724709369995...), and when you get to ∞, you get (apparently), e.

Another thing, if a gambler plays a game with a probability of winning of n, n times, for a n that goes up to infinity, the probability of losing every bet is 1/e.
And the following gives e too:
  ∞
  Σ  1/k!
k=0
  ∞
  Σ  ((k-1)²)/k!
k=0
  ∞
  Σ  (2k+1)/(2k)!
k=0
∞
1/2(Σ (k+1)/k!)
     k=0
∞
Σ   (k^2-2k+1)/k!
k=0
∞
(Σ  ((z-1+k)/k!))/z, where z is any real number (or complex)
k=0
∞
3-(Σ (k+1)/(k+3)!)
  k=0
  ∞
  Σ  ((3k)^2+1)/(3k)!
k=0
Also, e is equal to:
1/(2+1/(1+1/(2+1/(1+1/(1+1/(4+1/(1+1/(1+1/(6+1/(1+1/(1+1/(8+1/(1+1/(1+1/(10+1/...)))))))))))))))
Get the pattern?
And it is known that (in radians) e^(ix)=cos(x)+i(sin(x)) (which is the base for e^{(i^π)}=-1, but that's another story).
And the biggest non-complex value for x^(1/x) is at e.
So e isn't just a bunch of equations, but is the base for a lot of important equations.
-The Roaring Thunder

M2C2A: Episode 6⅓: Pi, a three part mathematical journey through the mathematical constant we all know and love, Part 2

[This proof is actually held by vihart, and shared by me, while the extra comes from Spanish Wikipedia, which inspired me to look for more digits of the not periodical sequence, which I found in http://mathworld.wolfram.com/PiContinuedFraction.html.]
Get a square, and draw a circle that touches all sides of the square

Let's say that the square's sides all measure 1.
Now modify the sides like this

so while the perimeter is still 4, now the circle is touched in 8 areas.
Modify it again and again, until you get...
A circle !
But is this REALLY a circle?
Nope!
A real circle has 0 sides, not ∞ like on this infinitely wrinkled circle.
So it is not a real circle, but an infinitely close imitation.
But what is the perimeter (remember this is an infinitely wrinkled circle with no curves, but ∞ sides)?
We started with 4, and by only modifying the sides, we didn't change the perimeter, only to get a final 4 as the perimeter!
So pi isn't four as anyone would have thought with this proof about making an imitation of a circle at first sight.
Extra:
Pi as a continued fraction?
To get pi to an accuracy of 11 digits, try "3+(1/(7+(1/(15+(1/(1+(1/(292+(1/(1+(1/(1+(1/(1+(1/(2+(1/3)))))))))))))))))", and continue the pattern with more digits I found here!
This is a great approximation, but can't you simply say 3.14159265358979.../1?
Not so exiting, but if you aren't worried about all numbers in the equation being integers, more understandable.
-The Roaring Thunder

M2C2A: Episode 6⅔: Pi: A three part mathematic

Me comenta mi Roaring Thunder, que me faltó publicar esta entrega, por lo que arreglo mi error y les comparto el episodio 6 dos tercios
Is pi random?
Nobody knows, but it looks random enough.
First of all: though pi will never change, randomness is still valid.
Second: Let's try to approve or not approve randomness.
One of the properties of randomness is that there are an approximately equal number of appearances of each of the possibilities (here 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0). If you check in the digits of pi, you'll find this property true. Want to check it? Try going to this page and use Ctrl+F. ✓
Another property of randomness, though identical to the first in concept, but referring to the sequences of digits is also something you can try in the page of the last hyperlink, and with some short sequences, you will find it also true. ✓
You may start calling pi random, but we're still not sure. We need to know more digits to see if no sequences appear in the total of all pi digits (after all, you'd never know if a house is a house if you check atom by atom). So final answer?
MAYBE.
-The Roaring Thunder

M2C2A: Episode 14, What is 0^0? Let's unscramble this nonsense once in for all!

What is 0⁰? And I'm not expecting some miracle answer or nothing, I'm expecting the truth. And actually, it's much more complex than you might think (and I'm not talking about i here).

My point is, powers with base 0 (0ⁿ) could be forbidden.

It is known that x^m*xⁿ=x^(m+n).

But also that x^m/xⁿ=x^(m-n).

So if you might call 0² as 0, or 0³, you would be forced to say 0³/0², that is 0¹, would be 0/0.

But there is something wrong about that.

Remember when we talked about 0/0? It could even be 0!

But we know that when we say 0¹, we're talking about a number that when you multiply 1 zero together (that is, leave it as it was), you're talking about 0! So 0/0 is 0 in this case.

But 0⁰ has nothing to forbid it.

The only reason mathematicians called n⁰ as 1, was because n¹ =(n)/n¹, (that is n^(1-1)=n⁰) was always 1... except for 0.

So the only thing that can define without barriers 0^0 is... Our number with infinite answers! 0/0! (or 0j, if you remember one of our last episodes)! But of course because almost everyone else believes 0/0 is undefined, 0⁰ is as undefined as.

-The Roaring Thunder

M2C2A: Episode 13, ∞, what has always been wrong about it

Many say ∞+1, ∞², or ∞-10^(10^(10^(10^10))), are simply ∞, but no.

∞ is like i, you (usually) can't simplify things with it. E.g.
If ∞+∞ is ∞, then we would be obliged to say ∞-∞=∞.

Is it?

We can use something I like to abbreviate as P.I.G (Patterns In Graphs, which can also refer to look for formulas), which is what I'll do.

If we graph x-x=y, we always get 0.

It's a truly linear equation.

We don't expect that when it gets to ∞ it will suddenly rise to ∞ too.
Same story with ∞*∞ and ∞/∞.

What makes sense in both cases, is that neither ∞+∞ or ∞*∞ should be expressed as ∞, but as 2∞, and ∞², respectively.

So ∞+1 should be written as it's written here, and so should 3/∞, 2^∞+1, x^y=y^∞x, or ∞x²+∞x+∞=0, etc.

...or is it?

This would work perfectly if it wasn't for the definition of ∞, the biggest quantity that can be described, which doesn't have an end.
If ∞+1>∞, then ∞+1 should be infinity!

But if ∞ (∞+1)<∞+1 (∞+2), then ∞+2 should be ∞!
But if this is smaller than ∞^∞(totally infinite!), then ∞^∞ SHOULD BE ∞!!!
So my definition of ∞ is:

nonsense.

M2C2A: Episode 12, The ABACABA, the biggest word in the mathematical dictionary

To write this word is a total mess, but to write the first 63 characters, this you can do.

Write an "a" every 2 spaces or (2¹) spaces. This should look like this:
a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a_a

Then, from the first unoccupied space, write a "b", every 4 spaces (2²) this time:

aba_aba_aba_aba_aba_aba_aba_aba_aba_aba_aba_aba_aba_aba_aba_aba

Repeat this last step, but with the "c", and now every 8 spaces (2³) .

abacaba_abacaba_abacaba_abacaba_abacaba_abacaba_abacaba_abacaba

If you continue the pattern, this you should get:

abacabadabacaba_abacabadabacaba_abacabadabacaba_abacabadabacaba
abacabadabacabaeabacabadabacaba_abacabadabacabaeabacabadabacaba
abacabadabacabaeabacabadabacabafabacabadabacabaeabacabadabacaba

Of course, if you continue this until the "z", you will get a word (2²⁷)-1 characters long, which is 134,217,727 letters long! 

And if you include all the character in the Unicode (the majority are Chinese characters and some are just representations as " ", but still, no discussing about that), the epic number of 109,449 you get:

5.40785978562894540705755027563290385780481607 × 10³²⁹⁴⁷ letters!!! 

But what does this apply to?

The Sierpiński Gasket!


Every time you see a black square, write "a", if you see a little white triangle, write "b", a bigger white triangle, "c"... etc.



And if all the "a"s in the triangle are one color, and the "b"s other... you get a colorful Sierpiński! (but that's another thing...)

And to really celebrate Sierpiński and the abacaba, I made the "rainbow gasket"!


Cool, huh?
-The Roaring Thunder

M2C2A: Episode 11, The root of a number?!

A square root of a number y is by definition a number x in which x² equals y. And a cube root of a number y is by definition a number x in which x³ equals y.
But we can also do n roots, in which the nth root of y is a number x in which which xⁿ equals y. But there's a special property about roots:

They may have many answers.

For example, the square root of 4.
2² is 4, but also -2². So can 2 and -2 be the roots of 4?
Yes!
Let's now take a different example:
The cube root of 8.
It may be true, but there are 2 more solutions.
First of all, you'll need to know complex numbers.
A complex number has a real part (2, 4, 7982) and an imaginary part, which can be any number times i.
But what is i?
i is the square root of -1, which doesn't exist, but can be used in many ways.
You can add i (23+i), subtract i (9-i), multiply i (23i) and divide i (i/5).
You can get i to the power of a number (i¹=1, i²=-1, i³=-i, and i⁴=1. This pattern repeats, and iⁿ=i^{n mod 4}).
So the second answer of the cube root of 8 is
-1 + 1.7320508075688772i and the third answer is -1-1.7320508075688772i.
And fourth roots?
Let's say we have the fourth root of 81. There are 4 answers for this:
A) 3
B) -3
C) 3i
D) -3i


We know that 3*3*3*3 is 81, and that -3*-3*-3*-3 is 81, but why 3i and -3i?
3i*3i is -9, because if the square root of -1 is i, then i² should be -1. And because 3*3 is 9, 9*-1 is -9, 3i² is -9. But we want 3i⁴, not 3i². So we square -9 to get 81. Same story with -3i.
So really, the root of a number is much more complex than you might think.
 
-The Roaring Thunder

M2C2A: Episode 10, Is 0 a prime???

Let's think of the definition: A number only divisible by 1 and itself. 0/1=0 ✓, but 0/0, itself is equal to...
Yes, calculators will tell you 0/0 is undefined, but if when we say x/y, you're looking for a number z that passes the test zy=x, so if x=0, and y=0, couldn't z be any number? 0×0=0, 0×1=0, 0×π=0, even 0×i^∞=0!
YES!

So 0/0=R∪C, that is, the union of the real and complex numbers.

Any number in or out of the number line can be 0/0, but isn't a number divisible by another when the number is an integer?
So because 0/0 can or can't be an integer, it is only SOMETIMES divisible by itself. So 0/0 is NOT completely divisible by itself, doesn't this seem strange?
We're dealing 0/0 as if we weren't dealing with something comparable with tan(90) or ∞^∞ .
So is it prime?
A little.

M2C2A: Episode 9, Goodbye Graham's number, you ain't big anymore.

What if we could make a number BIGGER than Graham's number, just for fun.
We'll call Graham's number G.
First of all, G+1.
Much more drastic, G*2.
Even greater, G^G. Or (G!)^(G!). 
But what if we invent some mathematical terms for a certainly bigger number, so, SO BIG, that by only writing the number of digits, of the NUMBER OF DIGITS, OF THE NUMBER OF DIGITS, YOU'D GET A NUMBER BIGGER THAN (((G!)!)!)!
How about we invent the "exponetorial"?
Let's write this as "¡".
This, instead of the factorial, which is 2*3*4*...n, goes 2^(3^(4^(5...n?))...)
So for example 2¡ would be 2,
3¡ would be 8,
4¡ would be 4,096,
5¡ would be 1,152,921,504,606,846,976, and
6¡ would be 2.3485425827738332278894805967893e+108!!! (the ! are exclamation signs).
7¡ would be 3.9408424552214162695348543183639e+758,
8¡ would be 5.8171811191842110297035069398346e+6068, and only
9¡ would be an overload for my 9.99999999999999999999999999999999e+9999 calculator!!!
How would we express G¡? And
(((((G¡)¡)¡)¡)¡)¡?!
Now, how about we try something definitively bigger than that.
Let's start with G¡. Now put G¡ "¡" after G (A.K.A G¡¡...¡¡¡, where the total number of "¡" is G¡). Let's call this G_1¡. 
Now let's make G_2¡ which will be G¡¡...¡¡¡, where the number of "¡" is now G_1¡. If you continue this to G_G¡, what will you get? An non-infinite number beyond what you could think possible!!!!! And G_G¡^G_G¡?! (Your brain can explode now).
-The Roaring Thunder

M2C2A: Episode 8, The magnitude of infinity.

The best way to see the magnitude of infinity, is to compare it with other big numbers and say "Infinity is bigger than that.". But with what big numbers?
In third place in the list of very big numbers, we have the googol (not to be confused with the Google searching machine), which is equivalent to 10¹⁰⁰ (A.K.A 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000), which is quite a big number.
In second place, we have the googolplex, equal to 10^googol (A.K.A "A number so big it couldn't be written because the observable universe isn't big enough").
But in first place, we have Graham's number, which is equal to this:
Suppose you want to write 3 cubed. You could say 3³, but you could also say 3↑3. But what if you wrote 3↑↑3? That would be 3 to the power of  3↑3. And 3↑↑↑3? This would be 3 to the power of 3↑↑3. But this is already 3^{7,625,597,484,987}! Why would someone need a number so ridiculously big?! Is this Graham's number?
Not even close.


We need 3↑↑↑↑3! And this isn't still Graham's number!!!
Now, let's call 3↑↑↑↑3 g_1. g_{1 is EXTREMELY BIG, but it is NOT Graham's number.}
Now, let's make g₂, where g₂ is equal to 3↑...↑3, and the number of arrows is g₁. Is this Graham's number?
Not by a googol of zeroes close (literally)!!!


Graham's number isn't achieved until g₆₄, and is so ridiculously large, that NOBODY KNOWS HOW MANY DIGITS IT HAS NOR IN WHICH DIGIT DOES IT START.
But this has nothing to do with infinity, does it? But this is the point I wanted to talk about:
Next time you hear "Infinity", remember this:
"BIGGER THAN GRAHAM'S NUMBER".

-The Roaring Thunder

M2C2A: Episode 7, 1+1=10? Face the binary truth.

Binary.
While many people relate it with computers, which is true, for binary is used in computers, but what much people don't understand it's that binary's actually simpler than you may think.
The numbers go in this sequence:

---

0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
...

---

Understand the pattern? Here's a more easier way to express it. We'll use 0's as no's and 1's as yes's. If the sum of a number (including only this numbers, and no number being used more than one time) includes any of this numbers, we'll put a 1 (yes). Else, we'll put a 0 (no)

---

8  4  2  1  Number

---

0  0  0  1       1 0  0  1  0       2
0  0  1  1       3
0  1  0  0       4
0  1  0  1       5
0  1  1  0       6
0  1  1  1       7
1  0  0  0       8
1  0  0  1       9
1  0  1  0       10
1  0  1  1       11
1  1  0  0       12
1  1  0  1       13
1  1  1  0       14
1  1  1  1       15

---

But another interesting thing about binary is that you can do most mathematical operations just fine by only modifying the algorithm a little bit.
For example, adding 1+1 in the binary modification will give you 10, which translated into the decimal system, is actually a truth: 1+1=2. And 1+1 it's not the only thing you can add in binary.  We can also try:

---

Binary addition:                                                                              Decimal translation: 101+110=1011                                                                                                5+6=11
1100101+1110001=11010110                                                                 101+113=214

---

And if you can add, why shouldn't you subtract?

---

Binary subtraction:                                                                     Decimal translation: 1000001-1=1000000                                                                                   65-1=64
1010101010-101010101=101010101                                                     682-341=341

---

You should try to modify the addition and subtraction algorithms so you can add and subtract in binary, but can you modify the multiplication algorithm to binary? Yes!
This are some examples of binary multiplication:

---

Binary multiplication:                                                                 Decimal translation: 10x10=100                                                                                                      2x2=4
11010x11010=1010100100                                                                       26x26=676

---

And division:

---

Binary division:                                                                          Decimal translation: 110÷10=11                                                                                                     6÷2=3
1010100101010100101010÷10=101010010101010010                  2774314÷2=173394

---

And of course you can try powers, after all they're a kind of multiplication. So next time anyone says to you that binary is hard, you'll have something to explain.
 
-The Roaring Thunder

Ciencias en casa

No guardo muchos recuerdos de mi infancia, sin embargo los pocos que se han quedado indelebles, cada que retornan, me transportan a esa etapa sencilla y apacible de mi niñez.
Debo haber tenido menos de ocho años, y en esa época la televisión era un lujo y los pocos canales que había transmitían sólo una o dos horas de televisión para niños, por lo tanto las tardes calurosas las pasaba recostada en mi cama ojeando los libros que encontraba en la casa.
Y no había muchos libros, pero los pocos que teníamos eran fabulosos. Mi papá tenía una colección de libros de Readers Digest con historias clásicas, y por su trabajo nos consiguió enciclopedias como la Salvat
o la enciclopedia Colibrí.
No teníamos todos los tomos, pero con los que teníamos me divertí sin saber en ese momento que estaba aprendiendo.
También en esa  época, mi mamá guardaba aún sus libros de la preparatoria, los cuales estaban llenos de garabatos y jeroglíficos inentendibles.
Pero había uno sólo uno de ellos que contenía imágenes divertidas y explicaciones que me abrieron los ojos para entender el mundo en el que vivimos y cómo funcionan los seres vivos.
Era un libro de Biología.
Recuerdo que la cubierta era negra y al centro tenía una mariposa monarca. Y lo que más me gustaba era que dentro de sus páginas se encontraba una rosa que mi papá le había regalado a mi mamá  cuando eran novios y se había conservado disecada dentro de tan voluminoso ejemplar.
Así es que no sólo era un libro entretenido sino también romántico.
Ahí descubrí cómo Mendel había descubierto los principios de la genética, con sus observaciones y experimentos con chicharitos verdes y amarillos (ni siquiera conocía los chicharos amarillos).
También descubrí que no todos veíamos igual, con las pruebas de visión del Dr Shinobu Ishihara

Fue en ese tiempo cuando nació mi amor por la ciencia. Sin embargo fue un romance de lejecitos, puesto que finalmente al momento de elegir mi profesión, no le ví utilidad práctica en mi vida a estos conocimientos, o igual los tenía reprimidos.

Recuerdo que por un tiempo quise ser biologa marina, bueno realmente entrenadora de delfines, para poder trabajar en SeaWorld.
Pero ya aterrizándome en la realidad, era tan quisquillosa, que no podía acercarme a un pescado crudo, ni para cocinarlo, así es que mis pobres delfines se iban a morir de hambre conmigo.
Finalmente estudié Administración de Empresas y luego Finanzas y mi vida era feliz, todo era color de rosa, las ciencias sólo estában en los programas de televisión del fin de semana, hasta que nacieron mis hijos.
Hoy más que nunca, lo que los gringos llaman STEM (Science, Technology, Engineering, and Mathematics) es decir; Ciencias, Tecnología, Ingeniería y Matemáticas, son lo que mueven al mundo y han contribuido a los grandes descubrimientos, inventos y avances en la historia.
Y con mis hijos descubrí algo que explica perfectamente Neil Degrasse Tyson (uno de mis astrofísicos favoritos… junto a Carl Sagan)

“Todo niño es un científico”

“No puedo pensar en una actividad más humana, que realizar experimientos de ciencia. Piénsa en esto – ¿qué hacen los niños?… Voltean piedras, le arrancan pétalos a una rosa – explarn el medioambiente a través de la experimentación. Eso es lo que como seres humanos hacemos, y lo hacemos a mayor profundidad y mejor que cualquier otra especie con la que nos hemos encontrado en la tierra… Nos inclinamos más por explorar nuestro medio ambiente que disfrutar una poesía cuando somos pequeños – hacemos eso más tarde. Antes de que esto suceda, todo niño es un científico. Así es que cuando pienso en ciencia, pienso en una actividad verdaderamente humana – algo fundamental a nuestro ADN , algo que motiva a la curiosidad”.

Fuente: http://www.brainpickings.org/index.php/2012/05/16/neil-degrasse-tyson-on-science/

-Neil Degrasse Tyson on Science

Con esto en mente, las ciencias en esta casa no se estudian, se viven, se promueven y se disfrutan. Y por lo tanto, los libros que ocupamos para “descubir” la Física, la Química y la Biología, son libros que como el de Biología de mi mamá (que tristemente ya no supe dónde quedó), no sólo cuentan una historia, sino que con imágenes y palabras invitan a descubrir y comprender el mundo, promueven el pensamiento crítico y el razonamiento y son un deleite al abrirlos, no importa la edad del individuo.

Mañana les compartiré los datos de estos libros.

Saludos!

- Eva

M2C2A: Episode 6, Pi: A three part mathematical journey through the mathematical constant we all know and love, Part 1

 

Image source: Wikipedia

We've all heard about π in any random moment in our lives, but getting down to brass tacks: "What is π?" is a more complicated question.
To answer it, I'll answer the following:
1. What's so special about the circle 〇?
2. Can we imitate a circle that it's circumference is not π?
3. Can we find sequences in the digits of π?
1. Answer:
A circle is special because it has not infinity sides, but it has none.
In such way, there are infinite curves inside every curve in a circle, making the circle a kind of fractal, where there's a curve inside the curve inside the curve inside the...
To calculate the circumference, π must be used in a way that helps us do it.
But why π?
π is used in circles and spheres for a reason, and it's because it was MADE in such way to do it.
And circles and spheres, including ovals, are ones of the only geometrical shapes that use pi to calculate their area/circumference/volume.
But to what point are we getting with this?
Circles are special because they depend on π.
Extra:
How to enter a circle (〇) on the keyboard.


First go to Google translate (sorry it's in Spanish), and choose Chinese.
Check the box that says "phonetic writing" and write "ling".
Click the down arrow two times and the right arrow two times more, and press space.
Copy and paste, and you have a circle (definition in Chinese: Unofficial way of saying 0.).
- The Roaring Thunder…